Useful one-function R packages, big data solutions, and a message from Yoda

Written on May 10, 2018 by Eduardo García-Portugués

Some simple and useful R packages
Handling big data in R
- The ff and ffbase packages
- Regression using biglm and friends
ASCII fun in R
- Text-based graphs with txtplot
- Cute animals with cowsay

Abstract

As the title reads, in this heterogeneous session we will see three topics of different interest. The first is a collection of three simple and useful one-function R packages that I use regularly in my coding workflow. The second collects some approaches to handling and performing linear regression with big data. The third brings in the freaky component: it presents tools to display graphical information in plain ASCII, from bivariate contours to messages from Yoda!

You can download the script with the R code alone here (right click and “Save as…”).

Required packages

We will need the following packages:

install.packages(c("viridis", "microbenchmark", "multcomp", "manipulate", 
                   "ffbase", "biglm", "leaps", "txtplot", "NostalgiR",
                   "cowsay"), 
                 dependencies = TRUE)

Some simple and useful `R` packages

Color palettes with `viridis`

Built-in color palettes in base R are somehow limited. We have rainbow, topo.colors, terrain.colors, heat.colors, and cm.colors. We also have flexibility to create our own palettes, e.g. by using colorRamp. These palettes look like:

# MATLAB's color palette
jet.colors <- colorRampPalette(c("#00007F", "blue", "#007FFF", "cyan",
                                 "#7FFF7F", "yellow", "#FF7F00", "red", 
                                 "#7F0000"))
# Plot for palettes
testPalette <- function(col, n = 200, ...) {
  image(1:n, 1, as.matrix(1:n), col = get(col)(n = n, ...), 
        main = col, xlab = "", ylab = "", axes = FALSE)
}

# Color palettes comparison
par(mfrow = c(2, 3))
res <- sapply(c("rainbow", "topo.colors", "terrain.colors", 
                "heat.colors", "cm.colors", "jet.colors"), testPalette)

center

Notice that some palettes clearly show non-uniformity in the color gradient. This potentially leads to an interpretation bias when inspecting heatmaps colored by these scales: some features are (unfairly) weakened and others are (unfairly) strengthen. This distortion on the representation of the data can be quite misleading.

In addition to these problems, some problematic points that are not usually thought when choosing a color scale are:

How does your pretty color image look like when you print it in black-and-white?
How do colorblind people read the images?

The package viridisLite (a port from Python’s Matplotlib) comes to solve these three issues. It provides the viridis color palette, which uses notions from color theory to be as much uniform as possible, black-and-white-ready, and colorblind-friendly. From viridisLite’s help:

This color map is designed in such a way that it will analytically be perfectly perceptually-uniform, both in regular form and also when converted to black-and-white. It is also designed to be perceived by readers with the most common form of color blindness.

More details can be found in this great talk by one of the authors:

There are several palettes in the package. All of them have the same properties as viridis (i.e., perceptually-uniform, black-and-white-ready, and colorblind-friendly). The cividis is specifically aimed to people with color vision deficiency. Let’s see them in action:

library(viridisLite)
# Color palettes comparison
par(mfrow = c(2, 3))
res <- sapply(c("viridis", "magma", "inferno", "plasma", "cividis"), 
              testPalette)

center

Some useful options for any of the palettes are:

# Reverse palette
par(mfrow = c(1, 2))
testPalette("viridis", direction = 1)
testPalette("viridis", direction = -1)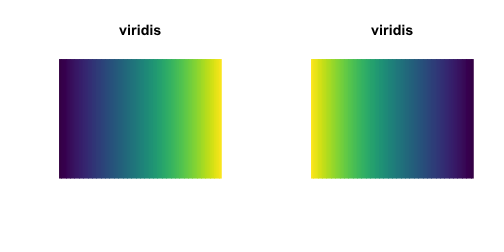

center

# Truncate color range
par(mfrow = c(1, 2))
testPalette("viridis", begin = 0, end = 1)
testPalette("viridis", begin = 0.25, end = 0.75)

center

# Asjust transparency
par(mfrow = c(1, 2))
testPalette("viridis", alpha = 1)
testPalette("viridis", alpha = 0.5)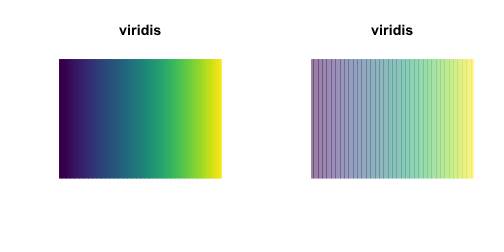

center

In the extended viridis package there are color palettes functions for ggplot2 fans: scale_color_viridis and scale_fill_viridis. Some examples of their use:

library(viridis)
library(ggplot2)

# Using scale_color_viridis
ggplot(mtcars, aes(wt, mpg)) + 
  geom_point(size = 4, aes(color = factor(cyl))) +
  scale_color_viridis(discrete = TRUE) +
  theme_bw()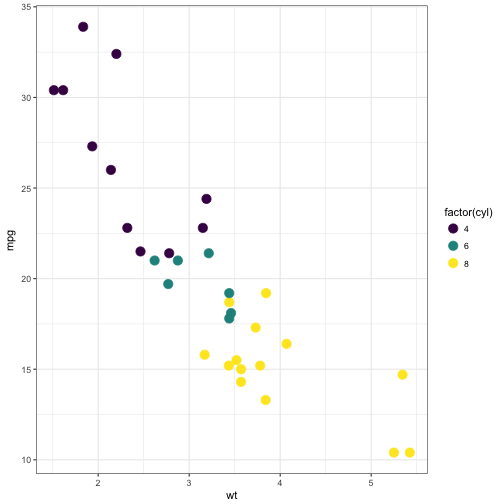

center

# Using scale_fill_viridis
dat <- data.frame(x = rnorm(1e4), y = rnorm(1e4))
ggplot(dat, aes(x = x, y = y)) +
  geom_hex() + coord_fixed() +
  scale_fill_viridis() + theme_bw()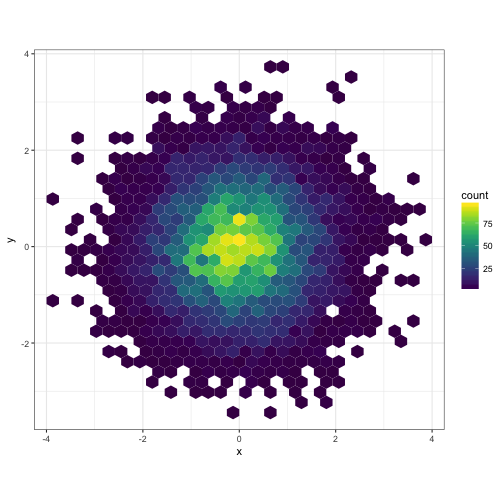

center

Benchmarking with `microbenchmark`

Measuring the code performance is a day-to-day routine for many developers. It is also a requirement for regular users that want to choose the most efficient coding strategy for implementing a method.

As we know, we can measure running times in base R using proc.time or system.time:

# Using proc.time
time <- proc.time()
for (i in 1:100) rnorm(100)
time <- proc.time() - time
time # elapsed is the 'real' elapsed time since the process was started

##    user  system elapsed 
##   0.004   0.000   0.003

# Using system.time - a wrapper for the above code
system.time({for (i in 1:100) rnorm(100)})

##    user  system elapsed 
##   0.003   0.000   0.003

However, this very basic approach presents several inconveniences to be aware of:

The precision of proc.time is within the millisecond. This means that evaluating 1:1000000 (usually) takes 0 seconds at the sight of proc.time.
Each time measurement of a procedure is subjected to variability (depends on the processor usage at that time, processor warm-up, memory status, etc). So, one single call is not enough to assess the time performance, several must be made (conveniently) and averaged.
It is cumbersome to check the times for different expressions. We will need several lines of code for each and creating auxiliary variables.
There is no summary of the timings. We have to code it by ourselves.
There is no checking on the equality of the results outputted from different approaches (accuracy is also important, not only speed!). Again, we have to code it by ourselves.

Hopefully, the microbenchmark package fills in these gaps. Let’s see an example of its usage on approaching a common problem in R: how to recentre a matrix by columns, i.e., how to make each column to have zero mean. There are several possibilities to do so, with different efficiencies.

# Data and mean
n <- 3
m <- 10
X <- matrix(1:(n * m), nrow = n, ncol = m)
mu <- colMeans(X)
# We assume mu is given in the time comparisons

Time to think by yourself on the competing approaches! Do not cheat and do not look into the next chunk of code!

# SPOILER ALERT!
#
#
#
#
#
#
#
#
#
#
#
#
#

# Some approaches:

# 1) sweep
Y1 <- sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-")

# 2) apply (+ transpose to maintain the arrangement of X)
Y2 <- t(apply(X, 1, function(x) x - mu))

# 3) scale
Y3 <- scale(X, center = mu, scale = FALSE)

# 4) loop
Y4 <- matrix(0, nrow = n, ncol = m)
for (j in 1:m) Y4[, j] <- X[, j] - mu[j]
  
# 5) magic (my favourite!)
Y5 <- t(t(X) - mu)

Which one do you think is faster? Do not cheat and answer before seeing the output of the next chunk of code!

# Test speed
library(microbenchmark)
bench <- microbenchmark(
  sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-"), 
  t(apply(X, 1, function(x) x - mu)), 
  scale(X, center = mu, scale = FALSE), 
  {for (j in 1:m) Y4[, j] <- X[, j] - mu[j]; Y4},
  t(t(X) - mu)
)

# Printing a microbenchmark object gives a numerical summary
bench

## Unit: microseconds
##                                                     expr      min
##          sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-")   27.106
##                       t(apply(X, 1, function(x) x - mu))   25.869
##                     scale(X, center = mu, scale = FALSE)   30.546
##  {     for (j in 1:m) Y4[, j] <- X[, j] - mu[j]     Y4 } 1809.293
##                                             t(t(X) - mu)    5.475
##         lq       mean    median        uq       max neval cld
##    32.5985   40.74705   36.8545   46.6620   125.168   100  a 
##    33.0635   51.26332   40.1875   46.9645  1108.167   100  a 
##    41.5115   52.32801   50.6105   60.4620   132.956   100  a 
##  1980.4605 2308.61451 2111.5060 2267.6455 16728.332   100   b
##     6.8630    9.68068    8.4820   11.5620    26.314   100  a

# Notice the last column. It is only present if the package multcomp is present.
# It provides a statistical ranking (accounts for which method is significantly 
# slower or faster) using multcomp::cld
 
# Adjusting display
print(bench, unit = "ms", signif = 2)

## Unit: milliseconds
##                                                     expr    min     lq
##          sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-") 0.0270 0.0330
##                       t(apply(X, 1, function(x) x - mu)) 0.0260 0.0330
##                     scale(X, center = mu, scale = FALSE) 0.0310 0.0420
##  {     for (j in 1:m) Y4[, j] <- X[, j] - mu[j]     Y4 } 1.8000 2.0000
##                                             t(t(X) - mu) 0.0055 0.0069
##    mean median    uq    max neval cld
##  0.0410 0.0370 0.047  0.130   100  a 
##  0.0510 0.0400 0.047  1.100   100  a 
##  0.0520 0.0510 0.060  0.130   100  a 
##  2.3000 2.1000 2.300 17.000   100   b
##  0.0097 0.0085 0.012  0.026   100  a

# unit = "ns" (nanosecs), "us" ("microsecs"), "ms" (millisecs), "s" (secs)

# Graphical methods for the microbenchmark object
# Raw time data
par(mfrow = c(1, 1))
plot(bench, names = c("sweep", "apply", "scale", "for", "recycling"))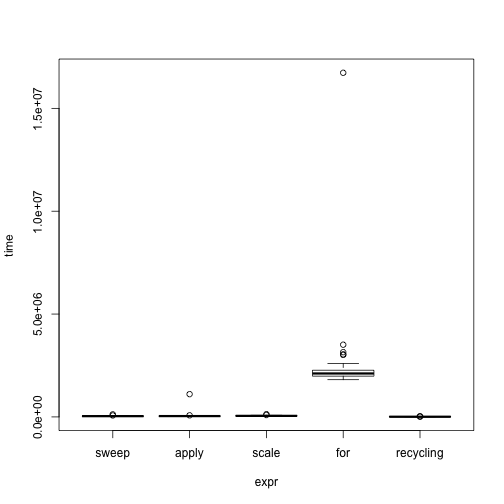

center

# Employs time logarithms
boxplot(bench, names = c("sweep", "apply", "scale", "for", "recycling"))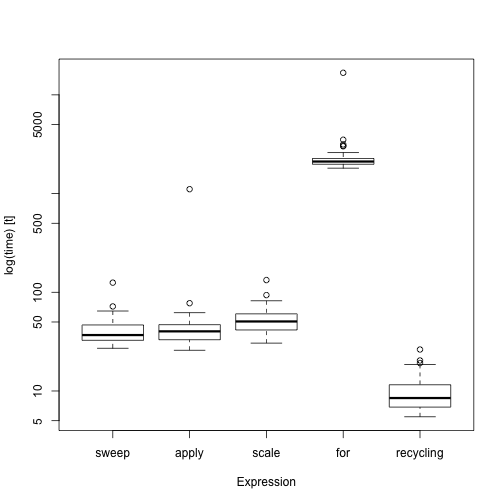

center

# Violin plots
autoplot(bench)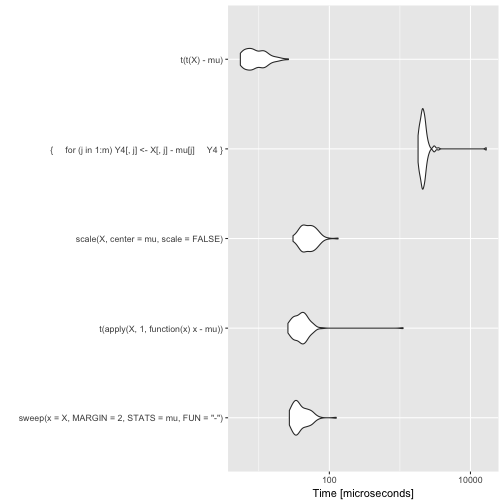

center

# microbenchmark uses 100 evaluations and 2 warmup evaluations (these are not 
# measured) by default. Here is how to change these dafaults:
bench2 <- microbenchmark(
  sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-"), 
  t(apply(X, 1, function(x) x - mu)), 
  scale(X, center = mu, scale = FALSE), 
  {for (j in 1:m) Y4[, j] <- X[, j] - mu[j]; Y4},
  t(t(X) - mu),
  times = 1000, control = list(warmup = 10)
)
bench2

## Unit: microseconds
##                                                     expr      min
##          sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-")   23.904
##                       t(apply(X, 1, function(x) x - mu))   22.755
##                     scale(X, center = mu, scale = FALSE)   29.752
##  {     for (j in 1:m) Y4[, j] <- X[, j] - mu[j]     Y4 } 1793.779
##                                             t(t(X) - mu)    5.174
##         lq       mean    median        uq       max neval cld
##    30.0340   56.16524   35.3675   48.0395 14865.043  1000  a 
##    29.8515   57.46285   37.8070   48.4140 14370.849  1000  a 
##    38.2395   53.72270   49.1660   64.1840   137.962  1000  a 
##  1982.3630 2368.55977 2101.0770 2276.9325 20275.055  1000   b
##     7.1435   11.03273    9.0750   13.5810    49.648  1000  a

# Let's check the accuracy of the methods as well as their timings. For that 
# we need to define a check function that takes as input a LIST with each slot
# representing the output of each method. The check must return TRUE or FALSE
check1 <- function (results) {
  all(sapply(results[-1], function(x) {
    max(abs(x - results[[1]]))
    }) < 1e-15) # Compares all results pair-wisely with the first
}

# Example with check function
bench3 <- microbenchmark(
  sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-"), 
  t(apply(X, 1, function(x) x - mu)), 
  scale(X, center = mu, scale = FALSE), 
  {for (j in 1:m) Y4[, j] <- X[, j] - mu[j]; Y4},
  t(t(X) - mu),
  check = check1
)
bench3

## Unit: microseconds
##                                                     expr      min
##          sweep(x = X, MARGIN = 2, STATS = mu, FUN = "-")   25.066
##                       t(apply(X, 1, function(x) x - mu))   23.126
##                     scale(X, center = mu, scale = FALSE)   30.813
##  {     for (j in 1:m) Y4[, j] <- X[, j] - mu[j]     Y4 } 1815.583
##                                             t(t(X) - mu)    5.258
##         lq       mean    median        uq       max neval cld
##    31.5470   39.70874   36.8125   44.3345   126.228   100  a 
##    28.2165   37.77894   33.2445   44.9965   155.791   100  a 
##    37.8560   51.20647   44.7735   57.8750   126.247   100  a 
##  1874.4285 2199.84572 1976.6860 2171.4360 16726.024   100   b
##     6.8515   10.44978    9.1005   12.9015    34.804   100  a

Quick animations with `manipulate`

The manipulate package (works only within RStudio!) allows to easily create simple animations. It is a simpler, local, alternative to Shiny applications.

library(manipulate)

# A simple example
manipulate({
  plot(1:n, sin(2 * pi * (1:n) / 100), xlim = c(1, 100), ylim = c(-1, 1),
       type = "o", xlab = "x", ylab = "y")
  lines(1:100, sin(2 * pi * 1:100 / 100), col = 2)
}, n = slider(min = 1, max = 100, step = 1, ticks = TRUE))

# Illustrating several types of controls using the kernel density estimator
manipulate({
  
  # Sample data
  if (newSample) {
    set.seed(sample(1:1000))
  } else {
    set.seed(12345678)
  }
  samp <- rnorm(n = n, mean = 0, sd = 1.5) 
  
  # Density estimate
  plot(density(x = samp, bw = h, kernel = kernel), 
       xlim = c(-x.rang, x.rang)/2, ylim = c(0, y.max))
  
  # Show data
  if (rugSamp) {
    rug(samp)
  }
  
  # Add reference density
  if (realDensity) {
    tt <- seq(-x.rang/2, x.rang/2, l = 200)
    lines(tt, dnorm(x = tt, mean = 0, sd = 1.5), col = 2)
  }
  },
  n = slider(min = 1, max = 250, step = 5, initial = 10),
  h = slider(0.05, 2, initial = 0.5, step = 0.05),
  x.rang = slider(1, 10, initial = 6, step = 0.5),
  y.max = slider(0.1, 2, initial = 0.5, step = 0.1),
  kernel = picker("gaussian", "epanechnikov", "rectangular", 
                  "triangular", "biweight", "cosine", "optcosine"),
  rugSamp = checkbox(TRUE, "Show rug"),
  realDensity = checkbox(TRUE, "Draw real density"),
  newSample = button("New sample!")
  )

# Another example: rotating 3D graphs without using rgl

# Mexican hat
x <- seq(-10, 10, l = 50)
y <- x
f <- function(x, y) {r <- sqrt(x^2 + y^2); 10 * sin(r)/r}
z <- outer(x, y, f)

# Colors
nrz <- nrow(z)
ncz <- ncol(z)
zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz]
col <- viridis(100)
facetcol <- cut(zfacet, length(col))
col <- col[facetcol]

# 3D plot
manipulate(
  persp(x, y, z, theta = theta, phi = phi, expand = 0.5, col = col,
        ticktype = "detailed", xlab = "X", ylab = "Y", zlab = "Sinc(r)"),
  theta = slider(-180, 180, initial = 30, step = 5),
  phi = slider(-90, 90, initial = 30, step = 5))

Handling big data in `R`

The `ff` and `ffbase` packages

R stores all the data in RAM, which is where all the processing takes place. But when the data does not fit into RAM (e.g., vectors of size $2\times 10^9$), alternatives are needed. ff is an R package for working with data that does not fit in RAM. From ff’s description:

The ff package provides data structures that are stored on disk but behave (almost) as if they were in RAM by transparently mapping only a section (pagesize) in main memory - the effective virtual memory consumption per ff object.

The package ff lacks some standard statistical methods for operating with ff objects. These are provided by ffbase.

Let’s see an example.

# Not really "big data", but for the sake of illustration
set.seed(12345)
n <- 1e6
p <- 10
beta <- seq(-1, 1, length.out = p)^5

# Data for linear regression
x1 <- matrix(rnorm(n * p), nrow = n, ncol = p)
x1[, p] <- 2 * x1[, 1] + rnorm(n, sd = 0.1)
x1[, p - 1] <- 2 - x1[, 2] + rnorm(n, sd = 0.5)
y1 <- 1 + x1 %*% beta + rnorm(n)
bigData1 <- data.frame("resp" = y1, "pred" = x1)

# Data for logistic regression
x2 <- matrix(rnorm(n * p), nrow = n, ncol = p)
y2 <- rbinom(n = n, size = 1, prob = 1 / (1 + exp(-(1 + x2 %*% beta))))
bigData2 <- data.frame("resp" = y2, "pred" = x2)

# Sizes of objects
print(object.size(bigData1), units = "Mb")

## 83.9 Mb

print(object.size(bigData2), units = "Mb")

## 80.1 Mb

# Save files to disk to emulate the situation with big data
write.csv(x = bigData1, file = "bigData1.csv", row.names = FALSE)
write.csv(x = bigData2, file = "bigData2.csv", row.names = FALSE)

# Read files using ff
library(ffbase) # Imports ff
bigData1ff <- read.table.ffdf(file = "bigData1.csv", header = TRUE, sep = ",")
bigData2ff <- read.table.ffdf(file = "bigData2.csv", header = TRUE, sep = ",")

# Recall: the *.csv are not copied into RAM!
print(object.size(bigData1ff), units = "Kb")

## 38.6 Kb

print(object.size(bigData2ff), units = "Kb")

## 38.7 Kb

# Delete the csv files in disk
file.remove(c("bigData1.csv", "bigData2.csv"))

## [1] TRUE TRUE

Operations on ff objects are carried out similarly as with regular data.frames:

# Operations on ff objects "almost" as with regular data.frames
class(bigData1ff)

## [1] "ffdf"

class(bigData1ff[, 1])

## [1] "numeric"

bigData1ff[1:5, 1] <- rnorm(5)
# See ?ffdf for more allowed operations

# Filter of data frames
ffwhich(bigData1ff, bigData1ff$resp > 5)

## ff (open) integer length=12943 (12943)
##     [1]     [2]     [3]     [4]     [5]     [6]     [7]     [8]         
##      32      86     341     377     437     440     688     747       : 
## [12936] [12937] [12938] [12939] [12940] [12941] [12942] [12943] 
##  999645  999720  999724  999780  999825  999833  999845  999885

Regression using `biglm` and friends

The richness of information returned by R’s lm has immediate drawbacks when working with big data (large $n$, $n>p$). An example is the following. If $n=10^8$ and $p=10$, simply storing the response and the predictors takes up to $8.2$ Gb in RAM. This is in the edge of feasibility for many regular laptops. However, calling lm will consume, at the very least, $16.5$ Gb merely storing the residuals, effects, fitted.values, and qr decomposition. Although there are more efficient ways of performing linear regression in base R (e.g., with .lm.fit), we still need to rethink the least squares estimates computation (takes $\mathcal{O}(np+p^2)$ in memory) to do not overflow the RAM.

A handy solution is given by the biglm package, which allows to fit a generalized linear model (glm) in R consuming much less RAM. Essentially, we have two possible approaches for fitting a glm:

Use a regular data.frame object to store the data, then use biglm to fit the model. This assumes that:
- We are able to store the dataset in RAM or, alternatively, that we can split it into chunks that are fed into the model iteratively, updating the fit via udpate for each new data chunk.
- The updating must rely only in the new chunk of data, not in the full dataset (otherwise, there is no point in chunking the data). This is possible with linear models, but not possible (at least exaclty) for generalized linear models.
Use a ffdf object to store the data, then use ffbase’s bigglm.ffdf to fit the model.

We will focus on the second approach due to its simplicity. For an example of the use of the first approach with a linear model, see here.

Let’s see first an example of linear regression.

library(biglm)
# bigglm.ffdf has a very similar syntax to glm - but the formula interface does 
# not work always as expected:
# bigglm.ffdf(formula = resp ~ ., data = bigData1ff) # Does not work
# bigglm.ffdf(formula = resp ~ pred.1 + pred.2, data = bigData1ff) # Does work, 
# but not very convenient for a large number of predictors

# Hack for automatic inclusion of all the predictors
f <- formula(paste("resp ~", paste(names(bigData1ff)[-1], collapse = " + ")))

# bigglm.ffdf's call
biglmMod <- bigglm.ffdf(formula = f, data = bigData1ff, family = gaussian())
class(biglmMod)

## [1] "bigglm" "biglm"

# lm's call
lmMod <- lm(formula = resp ~ ., data = bigData1)

# The reduction in size of the resulting object is more than notable
print(object.size(biglmMod), units = "Kb")

## 46.7 Kb

print(object.size(lmMod), units = "Mb")

## 358.6 Mb

# Summaries
s1 <- summary(biglmMod)
s2 <- summary(lmMod)
s1

## Large data regression model: bigglm(formula = f, data = bigData1ff, family = gaussian())
## Sample size =  1e+06 
##                Coef    (95%     CI)     SE      p
## (Intercept)  1.0021  0.9939  1.0104 0.0041 0.0000
## pred.1      -0.9732 -1.0132 -0.9332 0.0200 0.0000
## pred.2      -0.2866 -0.2911 -0.2821 0.0022 0.0000
## pred.3      -0.0535 -0.0555 -0.0515 0.0010 0.0000
## pred.4      -0.0041 -0.0061 -0.0021 0.0010 0.0000
## pred.5      -0.0002 -0.0022  0.0018 0.0010 0.8398
## pred.6       0.0003 -0.0017  0.0023 0.0010 0.7740
## pred.7       0.0026  0.0006  0.0046 0.0010 0.0090
## pred.8       0.0521  0.0501  0.0541 0.0010 0.0000
## pred.9       0.2840  0.2801  0.2880 0.0020 0.0000
## pred.10      0.9867  0.9667  1.0066 0.0100 0.0000

s2

## 
## Call:
## lm(formula = resp ~ ., data = bigData1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.8798 -0.6735 -0.0013  0.6735  4.9060 
## 
## Coefficients:
##               Estimate Std. Error  t value Pr(>|t|)    
## (Intercept)  1.0021454  0.0041200  243.236  < 2e-16 ***
## pred.1      -0.9732675  0.0199989  -48.666  < 2e-16 ***
## pred.2      -0.2866314  0.0022354 -128.227  < 2e-16 ***
## pred.3      -0.0534834  0.0009997  -53.500  < 2e-16 ***
## pred.4      -0.0040772  0.0009984   -4.084 4.43e-05 ***
## pred.5      -0.0002051  0.0009990   -0.205  0.83731    
## pred.6       0.0002828  0.0009989    0.283  0.77706    
## pred.7       0.0026085  0.0009996    2.610  0.00907 ** 
## pred.8       0.0520744  0.0009994   52.105  < 2e-16 ***
## pred.9       0.2840358  0.0019992  142.076  < 2e-16 ***
## pred.10      0.9866851  0.0099876   98.791  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9993 on 999989 degrees of freedom
## Multiple R-squared:  0.5777,	Adjusted R-squared:  0.5777 
## F-statistic: 1.368e+05 on 10 and 999989 DF,  p-value: < 2.2e-16

# The summary of a biglm object yields slightly different significances for the
# coefficients than for lm. The reason is that biglm employs N(0, 1) 
# approximations for the distributions of the t-tests instead of the exact 
# t distribution. Obviously, if n is large, the differences are inappreciable.

# Extract coefficients
coef(biglmMod)

##  (Intercept)       pred.1       pred.2       pred.3       pred.4 
##  1.002111877 -0.973211105 -0.286614434 -0.053495479 -0.004083508 
##       pred.5       pred.6       pred.7       pred.8       pred.9 
## -0.000201877  0.000286831  0.002610137  0.052073260  0.284048419 
##      pred.10 
##  0.986656286

# AIC
AIC(biglmMod, k = 2)

## [1] 998702.4

# Prediction works "as usual"
predict(biglmMod, newdata = bigData1[1:5, ])

##       [,1]
## 1 2.459090
## 2 2.797450
## 3 1.446842
## 4 1.601357
## 5 2.153806

# newdata must contain a column for the response!
# predict(biglmMod, newdata = bigData2[1:5, -1]) # Error

# Update the model with more training data - this is key for chunking the data
update(biglmMod, moredata = bigData1[1:100, ])

## Large data regression model: bigglm(formula = f, data = bigData1ff, family = gaussian())
## Sample size =  1000100

Model selection of biglm models can be done with the leaps package. This is achieved by the regsubsets function, which returns the best subset of up to (by default) nvmax = 8 predictors. The function requires the full biglm model to begin the “exhaustive” search, in which is crucial the linear structure of the estimator.

# Model selection adapted to big data models
library(leaps)
reg <- regsubsets(biglmMod, nvmax = p, method = "exhaustive")
plot(reg) # Plot best model (top row) to worst model (bottom row). Black color

center

# means that the predictor is included, white stands for excluded predictor

# Get the model with lowest BIC
subs <- summary(reg)
subs$which

##   (Intercept) pred.1 pred.2 pred.3 pred.4 pred.5 pred.6 pred.7 pred.8
## 1        TRUE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE
## 2        TRUE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE
## 3        TRUE  FALSE   TRUE  FALSE  FALSE  FALSE  FALSE  FALSE  FALSE
## 4        TRUE  FALSE   TRUE   TRUE  FALSE  FALSE  FALSE  FALSE  FALSE
## 5        TRUE  FALSE   TRUE   TRUE  FALSE  FALSE  FALSE  FALSE   TRUE
## 6        TRUE   TRUE   TRUE   TRUE  FALSE  FALSE  FALSE  FALSE   TRUE
## 7        TRUE   TRUE   TRUE   TRUE   TRUE  FALSE  FALSE  FALSE   TRUE
## 8        TRUE   TRUE   TRUE   TRUE   TRUE  FALSE  FALSE   TRUE   TRUE
## 9        TRUE   TRUE   TRUE   TRUE   TRUE  FALSE   TRUE   TRUE   TRUE
##   pred.9 pred.10
## 1  FALSE    TRUE
## 2   TRUE    TRUE
## 3   TRUE    TRUE
## 4   TRUE    TRUE
## 5   TRUE    TRUE
## 6   TRUE    TRUE
## 7   TRUE    TRUE
## 8   TRUE    TRUE
## 9   TRUE    TRUE

subs$bic

## [1] -558597.7 -837849.2 -854049.3 -856882.0 -859573.4 -861924.3 -861927.2
## [8] -861920.2 -861906.5

subs$which[which.min(subs$bic), ]

## (Intercept)      pred.1      pred.2      pred.3      pred.4      pred.5 
##        TRUE        TRUE        TRUE        TRUE        TRUE       FALSE 
##      pred.6      pred.7      pred.8      pred.9     pred.10 
##       FALSE       FALSE        TRUE        TRUE        TRUE

An example of logistic regression:

# Same comments for the formula framework - this is the hack for automatic
# inclusion of all the predictors
f <- formula(paste("resp ~", paste(names(bigData2ff)[-1], collapse = " + ")))

# bigglm.ffdf's call
bigglmMod <- bigglm.ffdf(formula = f, data = bigData2ff, family = binomial())

# glm's call
glmMod <- glm(formula = resp ~ ., data = bigData2, family = binomial())

# Compare sizes
print(object.size(bigglmMod), units = "Kb")

## 173.1 Kb

print(object.size(glmMod), units = "Mb")

## 679.2 Mb

# Summaries
s1 <- summary(bigglmMod)
s2 <- summary(glmMod)
s1

## Large data regression model: bigglm(formula = f, data = bigData2ff, family = binomial())
## Sample size =  1e+06 
##                Coef    (95%     CI)     SE      p
## (Intercept)  0.9960  0.9906  1.0015 0.0027 0.0000
## pred.1      -0.9970 -1.0028 -0.9911 0.0029 0.0000
## pred.2      -0.2839 -0.2890 -0.2789 0.0025 0.0000
## pred.3      -0.0533 -0.0583 -0.0483 0.0025 0.0000
## pred.4      -0.0015 -0.0065  0.0035 0.0025 0.5466
## pred.5      -0.0020 -0.0070  0.0030 0.0025 0.4201
## pred.6       0.0029 -0.0021  0.0079 0.0025 0.2465
## pred.7       0.0035 -0.0015  0.0085 0.0025 0.1584
## pred.8       0.0529  0.0479  0.0579 0.0025 0.0000
## pred.9       0.2821  0.2770  0.2871 0.0025 0.0000
## pred.10      0.9962  0.9903  1.0021 0.0029 0.0000

s2

## 
## Call:
## glm(formula = resp ~ ., family = binomial(), data = bigData2)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.5073  -0.8193   0.4306   0.7691   3.0466  
## 
## Coefficients:
##              Estimate Std. Error  z value Pr(>|z|)    
## (Intercept)  0.996049   0.002707  367.986   <2e-16 ***
## pred.1      -0.996951   0.002931 -340.134   <2e-16 ***
## pred.2      -0.283919   0.002535 -112.021   <2e-16 ***
## pred.3      -0.053271   0.002496  -21.340   <2e-16 ***
## pred.4      -0.001504   0.002494   -0.603    0.547    
## pred.5      -0.002011   0.002494   -0.806    0.420    
## pred.6       0.002889   0.002493    1.159    0.246    
## pred.7       0.003519   0.002495    1.411    0.158    
## pred.8       0.052924   0.002495   21.216   <2e-16 ***
## pred.9       0.282086   0.002531  111.466   <2e-16 ***
## pred.10      0.996187   0.002933  339.625   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1265999  on 999999  degrees of freedom
## Residual deviance:  974224  on 999989  degrees of freedom
## AIC: 974246
## 
## Number of Fisher Scoring iterations: 5

# AIC
AIC(bigglmMod, k = 2)

## [1] 974246.3

# Prediction works "as usual"
predict(bigglmMod, newdata = bigData2[1:5, ], type = "response")

##        [,1]
## 1 0.4330916
## 2 0.9237983
## 3 0.2420483
## 4 0.9619891
## 5 0.5443102

# predict(bigglmMod, newdata = bigData2[1:5, -1]) # Error

ASCII fun in `R`

Text-based graphs with `txtplot`

When evaluating R in a terminal with no possible graphical outputs (e.g. in a supercomputing cluster), it may be of usefulness to, at least, visualize some simple plots in a rudimentary way. This is what the txtplot and the NostalgiR package do, by means of ASCII graphics that are equivalent to some R functions.

`R` graph	ASCII analogue
`plot`	`txtplot`
`boxplot`	`txtboxplot`
`barplot(table())`	`txtbarchart`
`curve`	`txtcurve`
`acf`	`txtacf`
`plot(density())`	`nos.density`
`hist`	`nos.hist`
`plot(ecdf())`	`nos.ecdf`
`qqnorm(); qqline()`	`nos.qqnorm`
`qqplot`	`nos.qqplot`
`contour`	`nos.contour`
`image`	`nos.image`

Let’s see some examples.

library(txtplot) # txt* functions

# Generate common data
x <- rnorm(100)
y <- 1 + x + rnorm(100, sd = 1)
let <- as.factor(sample(letters, size = 1000, replace = TRUE))

# txtplot
plot(x, y)

center

txtplot(x, y)

##    +------+-----------+-----------+-----------+-----------++
##  4 +                                    *              *   +
##    |                                        *   *   *   *  |
##    |                         *  *   ***    *            *  |
##  2 +                        **      * *  **    *   *       +
##    |                **      *     ****    * *    *         |
##    |               *  *   * ** *  * **** ***               |
##    |          *   *    *** *  *   * ****   **              |
##  0 +         *  *    *****  ***                            +
##    |       **           **    *    *    *                  |
##    |         *  *                                          |
## -2 +           *     *                                     +
##    |  *           *                                        |
##    +------+-----------+-----------+-----------+-----------++
##          -2          -1           0           1           2

# txtboxplot
boxplot(x, horizontal = TRUE)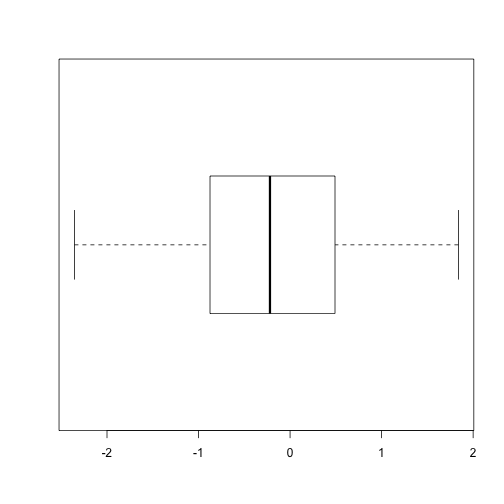

center

txtboxplot(x)

##        -2          -1           0            1           2  
##  |------+-----------+-----------+------------+-----------+-|
##                       +-------+-------+                     
##     ------------------|       |       |-----------------    
##                       +-------+-------+

# txtbarchart
barplot(table(let))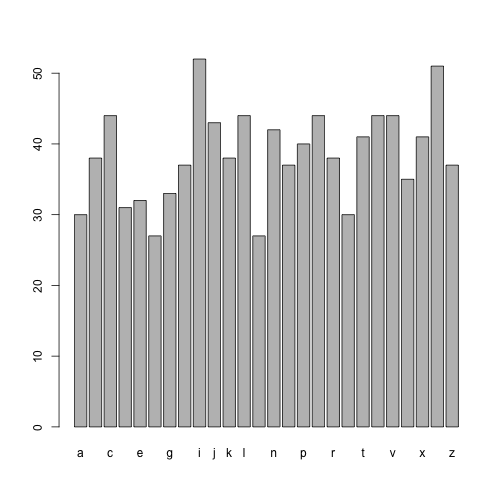

center

txtbarchart(x = let)

##   ++---------+---------+----------+---------+---------+----+
## 5 +                  *                                *    +
##   |      *           * *   *          *       * *     *    |
## 4 +      *           * *   *   *    * *     * * *   * *    +
##   |    * *         * * * * *   *  * * * *   * * * * * * *  |
## 3 +  * * * * *   * * * * * *   *  * * * * * * * * * * * *  +
##   |  * * * * * * * * * * * * * *  * * * * * * * * * * * *  |
## 2 +  * * * * * * * * * * * * * *  * * * * * * * * * * * *  +
##   |  * * * * * * * * * * * * * *  * * * * * * * * * * * *  |
## 1 +  * * * * * * * * * * * * * *  * * * * * * * * * * * *  +
##   |  * * * * * * * * * * * * * *  * * * * * * * * * * * *  |
## 0 +  * * * * * * * * * * * * * *  * * * * * * * * * * * *  +
##   ++---------+---------+----------+---------+---------+----+
##    0         5        10         15        20        25     
## Legend: 
## 1=a, 2=b, 3=c, 4=d, 5=e, 6=f, 7=g, 8=h, 9=i, 10=j, 11=k, 12=
## l, 13=m, 14=n, 15=o, 16=p, 17=q, 18=r, 19=s, 20=t, 21=u, 22=
## v, 23=w, 24=x, 25=y, 26=z

# txtcurve
curve(expr = sin(x), from = 0, to = 2 * pi)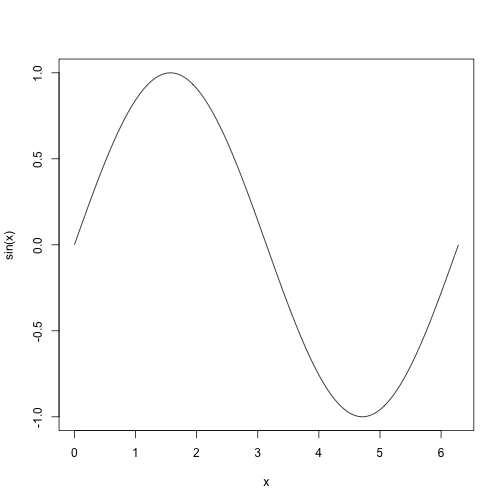

center

txtcurve(expr = sin(x), from = 0, to = 2 * pi)

##      +-+-------+-------+-------+-------+------+-------+----+
##    1 +          *********                                  +
##      |       ***        ***                                |
##      |      **             **                              |
##  0.5 +    **                **                             +
##      |   **                  **                            |
##      |  *                      *                           |
##    0 + *                        **                     **  +
##      |                           **                   **   |
## -0.5 +                             **                *     +
##      |                              **             **      |
##      |                                ***        ***       |
##   -1 +                                  *********          +
##      +-+-------+-------+-------+-------+------+-------+----+
##        0       1       2       3       4      5       6

# txtacf
acf(x)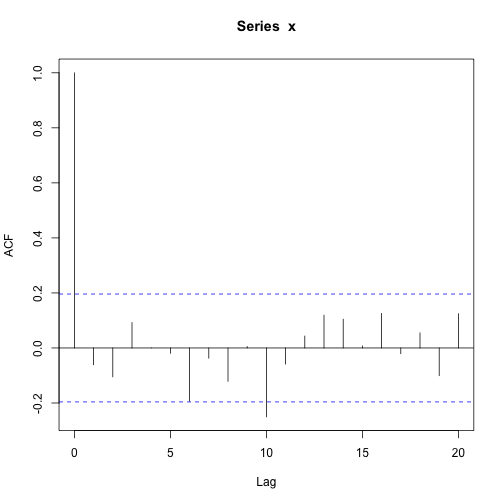

center

txtacf(x)

##      +-+------------+-----------+-----------+-----------+--+
##    1 + *                                                   +
##      | *                                                   |
##  0.8 + *                                                   +
##  0.6 + *                                                   +
##      | *                                                   |
##  0.4 + *                                                   +
##      | *                                                   |
##  0.2 + *                                                   +
##      | *       *                       *  *    *        *  |
##    0 + *  * *  * *  * *  * * *  * *  * *  * *  * *  * * *  +
##      |    * *         *    *    * *                   *    |
## -0.2 +                *         *                          +
##      +-+------------+-----------+-----------+-----------+--+
##        0            5          10          15          20

library(NostalgiR) # nos.* functions

# Mexican hat
xx <- seq(-10, 10, l = 50)
yy <- xx
f <- function(x, y) {r <- sqrt(x^2 + y^2); 10 * sin(r)/r}
zz <- outer(xx, yy, f)

# nos.density
plot(density(x)); rug(x)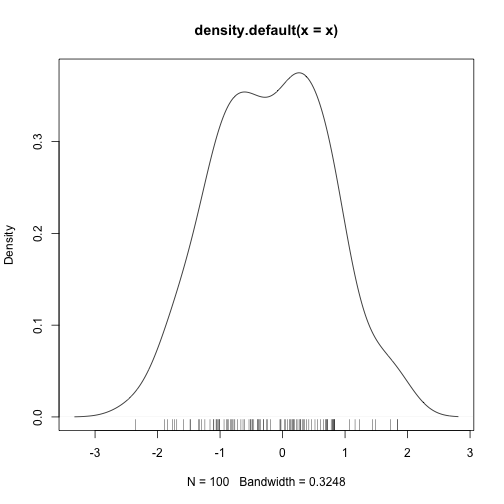

center

nos.density(x)

##       +----+-------+-------+------+-------+-------+-------++
##       |                     ~~~~~~~~~~~~                   |
##       |                    ~~          ~~                  |
##   0.3 +                   ~~            ~~                 +
## D     |                  ~~              ~                 |
## e     |                 ~~                ~                |
## n 0.2 +                ~~                 ~~               +
## s     |               ~~                   ~               |
## i     |              ~~                    ~~              |
## t 0.1 +             ~~                      ~~~            +
## y     |           ~~~                         ~~~          |
##       |         ~~~                             ~~~~       |
##     0 + ~~~~~~~~~   oooooooooooooooooooooo oo o oo ~~~~~~  +
##       +----+-------+-------+------+-------+-------+-------++
##           -3      -2      -1      0       1       2       3

# nos.hist
hist(x)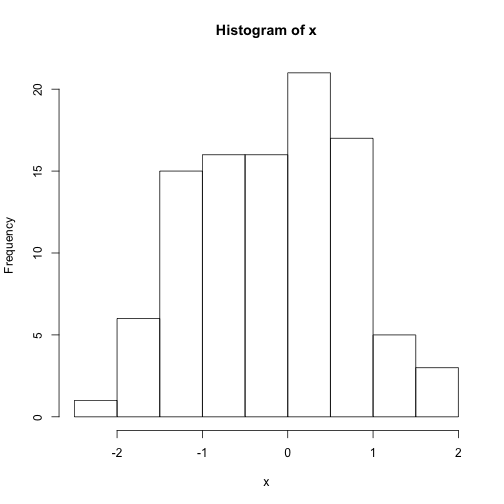

center

nos.hist(x)

##      +-----+-----------+-----------+-----------+-----------+
##   20 +                                o                    +
##      |                                o                    |
## F    |                    o     o     o     o              |
## r 15 +              o     o     o     o     o              +
## e    |              o     o     o     o     o              |
## q    |              o     o     o     o     o              |
## u 10 +              o     o     o     o     o              +
## e    |              o     o     o     o     o              |
## n    |        o     o     o     o     o     o              |
## c  5 +        o     o     o     o     o     o     o        +
## y    |        o     o     o     o     o     o     o     o  |
##    0 + o      o     o     o     o     o     o     o     o  +
##      +-----+-----------+-----------+-----------+-----------+
##           -2          -1           0           1

# nos.ecdf
plot(ecdf(x))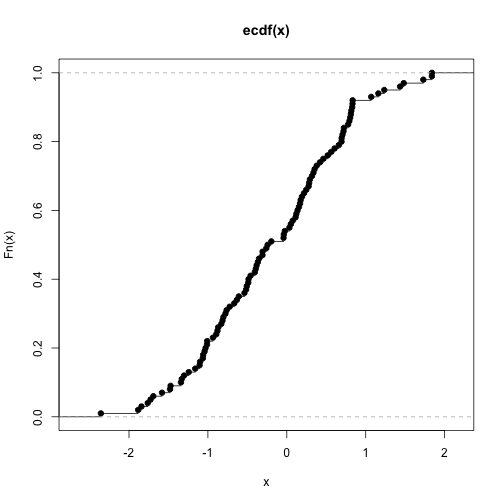

center

nos.ecdf(x)

##       +-----+-----------+----------+-----------+----------++
##     1 +                                         ooo~o~~oo  +
##       |                                     oo~~~          |
##   0.8 +                                  oooo              +
##       |                                ooo                 |
## E 0.6 +                              ooo                   +
## C     |                          o~ooo                     |
## D     |                        ooo                         |
## F 0.4 +                     oooo                           +
##       |                  oooo                              |
##   0.2 +                ooo                                 +
##       |            ooooo                                   |
##       | o~~~~~ooooo~                                       |
##     0 +-----+-----------+----------+-----------+----------++
##            -2          -1          0           1          2

# nos.qqnorm
qqnorm(x); qqline(x)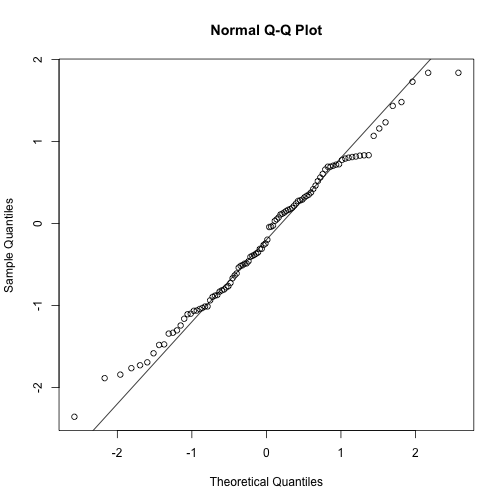

center

nos.qqnorm(x)

##    2 +-------+--------+---------+--------+---------+-------+
##      |                                           o~o~o  o  |
## S    |                                       ~ooo~         |
## a  1 +                                   oooooo            +
## m    |                               oooo~                 |
## p  0 +                          oooooo                     +
## l    |                       ~ooo~                         |
## e    |                   ~ooooo                            |
##   -1 +               oooooo                                +
## Q    |           ~oooo                                     |
## s    |     o o~ooo                                         |
##   -2 + o ~~~~~                                             +
##      +-------+--------+---------+--------+---------+-------+
##             -2       -1         0        1         2        
##                          Theoretical Qs

# nos.qqplot
qqplot(x, y)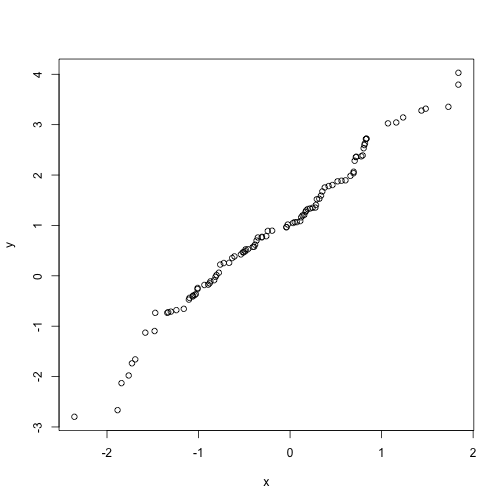

center

nos.qqplot(x, y)

##    +------+-----------+-----------+-----------+-----------++
##  4 +                                                    o  +
##    |                                           ooo oo  o   |
##    |                                       oo              |
##  2 +                                    oooo            ~  +
##    |                                oooo         ~~~~~~~   |
##    |                          ooo ooo     ~~~~~~~          |
##    |                     ooooo     ~~~~~~~                 |
##  0 +                 oooo   ~~~~~~~~                       +
##    |            o ooo~~~~~~~                               |
##    |          oo~~~~~                                      |
## -2 +   ~~~~~oo                                             +
##    |  o    o                                               |
##    +------+-----------+-----------+-----------+-----------++
##          -2          -1           0           1           2

# nos.contour
contour(xx, yy, zz)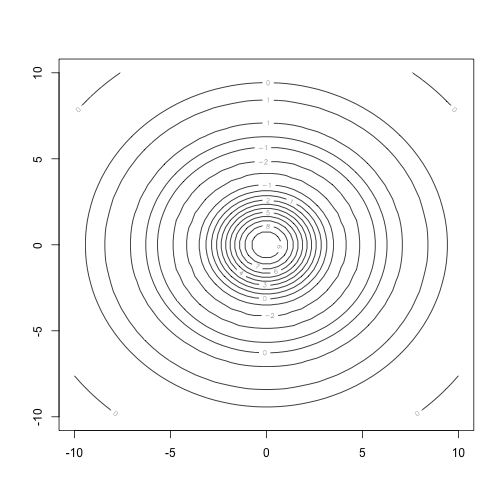

center

nos.contour(data = zz, xmin = min(xx), xmax = max(xx), 
            ymin = min(yy), ymax = max(yy))

##     +-+------------+-----------+------------+-----------+--+
##  10 +       33  22   22222 3333333333 22222  222  33       +
##     |   33332222222233333444444444444443333322222222333    |
##     | 333222 222333444444              444444333222 22233  |
##     |  222222333444    444444444444444444    444333222222  |
##   5 + 2 22233444   44443333222222222233334444   4443322 2  +
##     |   2 3344   444332 1111111111111111 233444   4433 2   |
##     | 22 3 44   44332111112345555554321111123344   44 3 2  |
##     |   3 44   4332 111134555      555431111 2334   4433   |
##     |   3 4   4 32 111 245            542 11  2344   4 3   |
##   0 +   3 4   4 32 111 245            542 11  2344   4 3   +
##     |   3 44   4332 111134555      555431111 2334   4433   |
##     | 22 3 44   43322111112345555554321111122344   44 3 2  |
##     |  2233344   444332111111111111111111233444   4433322  |
##  -5 + 2 22233444   44443332222111122223334444   4443322 2  +
##     |  222222333444    444444444444444444    444333222222  |
##     | 333222 222333444444              444444333222 22233  |
##     |   3333222 22223333344444444444444333332222 222333    |
## -10 +       33 222   22222 3333333333 22222  2222 33       +
##     +-+------------+-----------+------------+-----------+--+
##      -10          -5           0            5          10   
## Legend: 1 ~ -2.02; 2 ~ -0.769; 3 ~ -0.082; 4 ~ 0.795; 5 ~ 1.74

# nos.image
image(zz, col = viridis(50))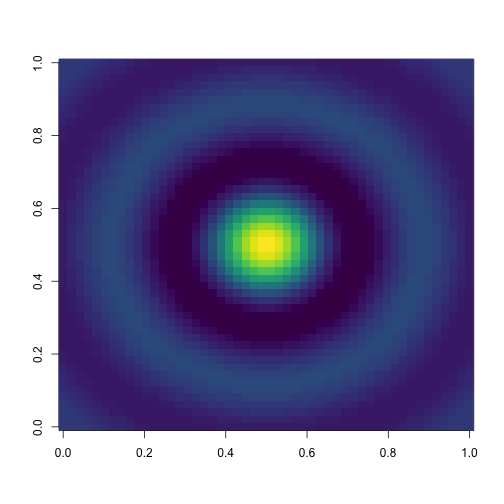

center

nos.image(data = zz, xmin = min(xx), xmax = max(xx), 
          ymin = min(yy), ymax = max(yy))

##     +-+------------+-----------+------------+-----------+--+
##  10 + o oooo........................................ooooo  +
##     | o oo....................oooo....................ooo  |
##     | . .............oooooooooooooooooooooo..............  |
##     | . .........oooooooooooooooooooooooooooooo..........  |
##   5 + . ......oooooooooo................oooooooooo.......  +
##     | . ....oooooooo........................oooooooo.....  |
##     | . ...oooooooo..........................oooooooo....  |
##     | . ..ooooooo..........oooxxxxooo..........ooooooo...  |
##     | . ..oooooo.........ooxXX####XXxoo.........oooooo...  |
##   0 + . .ooooooo........ooxXX######XXxoo........ooooooo..  +
##     | . ..ooooooo........ooxxXXXXXXxxoo........ooooooo...  |
##     | . ..oooooooo..........oooooooo..........oooooooo...  |
##     | . ...oooooooo..........................oooooooo....  |
##  -5 + . .....oooooooo......................oooooooo......  +
##     | . .......ooooooooooo............ooooooooooo........  |
##     | . ..........oooooooooooooooooooooooooooo...........  |
##     | o ...............oooooooooooooooooo...............o  |
## -10 + o ooo..........................................oooo  +
##     +-+------------+-----------+------------+-----------+--+
##      -10          -5           0            5          10   
## Legend: 
## . ~ (-2.17,0.235); o ~ (0.235,2.64); x ~ (2.64,5.05); X ~ (5
## .05,7.45); # ~ (7.45,9.86)

Cute animals with `cowsay`

cowsay is a package for printing messages with ASCII animals. Although it has little practical use, it is way fun! There is only one function, say, that produces an animal with a speech bubble.

library(cowsay)

# Random fortune
set.seed(363)
say("fortune", by = "random")

## 
##  ----- 
## If 'fools rush in where angels fear to tread', then Bayesians 'jump' in where frequentists fear to 'step'.
##  Charles C. Berry
##  about Bayesian model selection as an alternative to stepwise regression
##  R-help
##  November 2009 
##  ------ 
##     \   
##      \  
##       \
##             ,        ,
##            /(        )`
##            \ \___   / |
##             /- _  `-/  '
##            (/\/ \ \   /\
##            / /   | `    
##            O O   ) /    |
##            `-^--'`<     '
##           (_.)  _  )   /
##            `.___/`    /
##              `-----' /
## <----.     __ / __   \
## <----|====O)))==) \) /====
## <----'    `--' `.__,' \
##              |        |
##               \       /
##         ______( (_  / \______
##       ,'  ,-----'   |        \
##       `--{__________)        \/ [nosig]

# All animals
# sapply(names(animals), function(x) say(x, by = x))

# Annoy the users of your package with good old clippy
say(what = "It looks like you\'re writing a letter!", 
    by = "clippy", type = "warning")

## Warning in say(what = "It looks like you're writing a letter!", by = "clippy", : 
## 
##  ----- 
## It looks like you're writing a letter! 
##  ------ 
##     \   
##      \
##    __
##    / \
##    | |
##    @ @
##   || ||
##   || ||
##   |\_/|
##   \___/ GB

# A message from Yoda
say("Participating in the Coding Club UC3M you must. Yes, hmmm.", by = "yoda")

## 
## 
## 
##  ----- 
## Participating in the Coding Club UC3M you must. Yes, hmmm. 
##  ------ 
##     \   
##      \
##                    ____
##                 _.' :  `._
##             .-.'`.  ;   .'`.-.
##    __      / : ___\ ;  /___ ; \      __
##   ,'_ ""--.:__;".-.";: :".-.":__;.--"" _`,
##   :' `.t""--.. '<@.`;_  ',@>` ..--""j.' `;
##        `:-.._J '-.-'L__ `-- ' L_..-;'
##           "-.__ ;  .-"  "-.  : __.-"
##              L ' /.------.\ ' J
##              "-.   "--"   .-"
##              __.l"-:_JL_;-";.__
##          .-j/'.;  ;""""  / .'\"-.
##          .' /:`. "-.:     .-" .';  `.
##       .-"  / ;  "-. "-..-" .-"  :    "-.
##   .+"-.  : :      "-.__.-"      ;-._   \
##   ; \  `.; ;                    : : "+. ;
##   :  ;   ; ;                    : ;  : \:
##   ;  :   ; :                    ;:   ;  :
##   : \  ;  :  ;                  : ;  /  ::
##   ;  ; :   ; :                  ;   :   ;:
##   :  :  ;  :  ;                : :  ;  : ;
##   ;\    :   ; :                ; ;     ; ;
##   : `."-;   :  ;              :  ;    /  ;
##  ;    -:   ; :              ;  : .-"   :
##   :\     \  :  ;            : \.-"      :
##   ;`.    \  ; :            ;.'_..--  / ;
##   :  "-.  "-:  ;          :/."      .'  :
##    \         \ :          ;/  __        :
##     \       .-`.\        /t-""  ":-+.   :
##      `.  .-"    `l    __/ /`. :  ; ; \  ;
##        \   .-" .-"-.-"  .' .'j \  /   ;/
##         \ / .-"   /.     .'.' ;_:'    ;
##   :-""-.`./-.'     /    `.___.'
##                \ `t  ._  /  bug
##                 "-.t-._:'
##

Coding Club UC3M

Useful one-function R packages, big data solutions, and a message from Yoda

Some simple and useful R packages

Color palettes with viridis

Benchmarking with microbenchmark

Quick animations with manipulate

Handling big data in R

The ff and ffbase packages

Regression using biglm and friends

ASCII fun in R

Text-based graphs with txtplot

Cute animals with cowsay

Share this:

Related Posts

LSTM with Keras TensorFlow 27 Nov 2018

Online resources for teaching 06 Nov 2018

An introduction to Shiny II 16 Oct 2018

Some simple and useful `R` packages

Color palettes with `viridis`

Benchmarking with `microbenchmark`

Quick animations with `manipulate`

Handling big data in `R`

The `ff` and `ffbase` packages

Regression using `biglm` and friends

ASCII fun in `R`

Text-based graphs with `txtplot`

Cute animals with `cowsay`